I wrote a (very long) blog post about those viral math problems and am looking for feedback, especially from people who are not convinced that the problem is ambiguous.
It’s about a 30min read so thank you in advance if you really take the time to read it, but I think it’s worth it if you joined such discussions in the past, but I’m probably biased because I wrote it :)
If you are so sure that you are right and already “know it all”, why bother and even read this? There is no comment section to argue.
I beg to differ. You utter fool! You created a comment section yourself on lemmy and you are clearly wrong about everything!
You take the mean of 1 and 9 which is 4.5!
/j
🤣 I wasn’t even sure if I should post it on lemmy. I mainly wrote it so I can post it under other peoples posts that actually are intended to artificially create drama to hopefully show enough people what the actual problems are with those puzzles.
But I probably am a fool and this is not going anywhere because most people won’t read a 30min article about those math problems :-)
Actually the correct answer is clearly 0.2609 if you follow the order of operations correctly:
6/2(1+2)
= 6/23
= 0.26Nah man, distribute the 2.
6/2(1+2)
= 6/2+4
= 3+4
= 7This is like 4st grayed maff.
🤣 I’m not sure if you read the post but I also wrote about that (the paragraph right before “What about the real world?”)
I did read the post (well done btw), but I guess I must have missed that. And here I thought I was a comedic genius
@relevants you truly are the smartest of all men
I did (skimmed it, at least) and I liked it. 🙃
Right, because 5 rounds down to 4.5
@Prunebutt meant 4.5! and not 4.5. Because it’s not an integer we have to use the gamma function, the extension of the factorial function to get the actual mean between 1 and 9 => 4.5! = 52.3428 which looks about right 🤣
Not sure if sarcastic and woosh, or adding to the joke ಠ_ಠ
The mean of 1 and 9 is 5
woosh
I think you got hit hard by Poe’s Law here. Except it’s more like people couldn’t tell if you were jokingly or genuinely getting your math wrong… Even after you explained you were joking lol
I thought the “/j” tone-tag was enough ;_;
jarcasm?
If one doesn’t realize you’re op, the entire thing can be interpreted very differently.
Then “Not sure if sarcastic and woosh, or adding to the joke ಠ_ಠ” could be interpreted as something like “I’m not sure if you are adding to the joke and I’m not understanding it”.
Stop it Patrick, you’re scaring them!
…Because 4 rounds up to 4.5
The answer realistically is determined by where you place implicit multiplication (or “multiplication by juxtaposition”) in the order of operations.
Some place it above explicit multiplication and division, meaning it gets done before the division giving you an answer of 1
But if you place it as equal to it’s explicit counterparts, then you’d sweep left to right giving you an answer of 9
Since those are both valid interpretations of the order of operations dependent on what field you’re in, you’re always going to end up with disagreements on questions like these…
But in reality nobody would write an equation like this, and even if they did, there would usually be some kind of context (I.e. units) to guide you as to what the answer should be.
Edit: Just skimmed that article, and it looks like I did remember the last explanation I heard about these correctly. Yay me!
Exactly. With the blog post I try to reach people who already heared that some people say it’s ambiguous but either down understand how, or don’t believe it. I’m not sure if that will work out because people who “already know the only correct answer” probably won’t read a 30min blog post.
Unfortunately these types of viral problems are designed the attract people who think they “know it all”, so convincing them that their chosen answer isn’t as right as they think it is will always be an uphill challenge
Yeah, that’s why fractions are good thing.
yeah, our math profs taught if the 2( is to be separated from that bracket for the implied multiplication then you do that math first, because the 2(1+2) is the same as (1+2)+(1+2) and not related to the first 6.
So you were taught strong juxtaposition then, where the implicit multiplication takes priority?
if it was 6÷2x(2+1) they suggested do division and mult from left to right, but 6÷2(2+1) implied a relationship between the number outside the parenthesis and inside them, and as soon as you broke those () you had to do the multiplication immediately that is connected to them. Like some models of calculatora do. wasn’t till a few yeara ago that I heard people were doing it differently.
if it was 6÷2x(2+1) they suggested do division and mult from left to right, but 6÷2(2+1)
Correct! Terms are separated by operators and joined by grouping symbols, so 6÷2x(2+1) is 3 terms - 6, 2, and (2+1) - whereas 6÷2(2+1) is 2 terms - 6 and 2(2+1), and the latter term has a precedence of “brackets”, NOT “multiplication”. Multiplication refers literally to multiplication signs, which are only present in your first example (hence evaluated with a different order than your second example).
Also noted that the OP has ignored your comment, seeing as how you pointed out the unambiguous way to do it.
2(1+2) is the same as (1+2)+(1+2)
You nearly had it. 2(1+2) is the same as (2x1+2x2). The Distributive Law - it’s the reverse process to factorising.
implicit multiplication
There’s no such thing as “implicit multiplication”
Some place it above explicit multiplication and division,
Which is correct, seeing as how we’re solving brackets, and brackets always come first.
But if you place it as equal to it’s explicit counterparts, then you’d sweep left to right giving you an answer of 9
Which is wrong.
Since those are both valid interpretations of the order of operations
No, they’re not. Treating brackets as, you know, brackets, is the only valid interpretation. “Multiplication” refers literally to multiplication signs, of which there are none in this problem.
But in reality nobody would write an equation like this
Yes they would. a(b+c) is the standard way to write a factorised term.
Ackshually, the answer is 4
6÷2*(1+2)
6÷(1+2)*2
6÷(3)*2
2*2
4
You’re welcome
psychopath
Psychomath
c/TheyDidAMath
If there are rules about which dot comes first then you are not allowed to do this.
You aren’t allowed to do this because division isn’t transitive.
deleted by creator
In fact you’re not allowed to add the multiplication - it breaks up the factorised term, hence gives a different answer.
The rule is you’re not allowed to add dots (multiplication) - broke up the factorised term, which is why a different answer.
Typo in article:
If you are however willing to except the possibility that you are wrong.
Except should be ‘accept’.
Not trying to be annoying, but I know people will often find that as a reason to disregard academic arguments.
Thank you very much 🫶. No it’s not annoying at all. I’m very grateful not only for the fact that you read the post but also that you took the time to point out issues.
I just fixed it, should be live in a few minutes.
A person not knowing the difference in usage between except and accept sounds like a perfectly reasonable reason to disregard their math skills.
Especially when said person keeps making incorrect statements about Maths and ignores completely what is taught in high school.
academic arguments
The “academic arguments” can be ignored since this is actually high school Maths - it’s taught in Year 7-8.
Great write up! The answer is use parentheses or fractions and stop wasting everyone’s time 😅
What if the real answer is the friends we made along the way?
This is Facebook we are talking about, what friends? Everyone hates everyone on Facebook
That’d be good, but what I’ve found so far here is a whole bunch of people who don’t like being told the actual facts of the matter! 😂
deleted by creator
I love that the calculators showing different answers are both from the same manufacturer XD
My TI-84 Plus is my holy oracle, I will go with whatever it says.
And then get distracted and play some Doom.
It will give 9, just like my 89 emulator. It treats division like a fraction. For a TI, the entire denominator of a fraction needs to be in parentheses or you get into trouble.
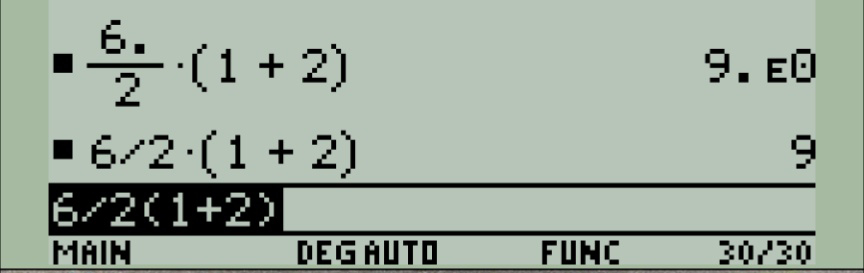
It treats division like a fraction
Which is why it gives the wrong answer.
Also you shouldn’t be adding a dot between the 2 and the brackets - that also changes the answer.
❤️
TI calcs give the wrong answer, and it’s in their manual why - they only follow the Primary School rule (“inside the brackets”), not the High School rule which supersedes it (The Distributive Law).
What’s especially wild to me is that even the position of “it’s ambiguous” gets almost as much pushback as trying to argue that one of them is universally correct.
Last time this came up it was my position that it was ambiguous and needed clarification and had someone accuse me of taking a prescriptive stance and imposing rules contrary to how things were actually being done. How asking a person what they mean or seeking clarification could possibly be prescriptive is beyond me.
Bonus points, the guy telling me I was being prescriptive was arguing vehemently that implicit multiplication having precedence was correct and to do otherwise was wrong, full stop.
👍 That was actually one of the reasons why I wrote this blog post. I wanted to compile a list of points that show as clear as humanity possible that there is no consensus here, even amongst experts.
That probably won’t convince everybody but if that won’t probably nothing will.
I wanted to compile a list of points that show as clear as humanity possible that there is no consensus here, even amongst experts
And I wrote a bunch of fact checks pointing out there is consensus amongst the actual experts - high school Maths teachers and textbook authors, the 2 groups who you completely ignored in your blog post.
When I went to college, I was given a reverse Polish notation calculator. I think there is some (albeit small) advantage of becoming fluent in both PEMDAS and RPN to see the arbitrariness. This kind of arguement is like trying to argue linguistics in a single language.
Btw, I’m not claiming that RPN has any bearing on the meme at hand. Just that there are different standards.
This comment is left by the HP50g crew.
It would be better if we just taught math with prefix or postfix notation, as it removes the ambiguity.
Ambiguity is fine. It would tedious to the point of distraction to enforce writing math without ambiguity. You make note of conventions and you are meant to realize that is just a convention. I’m amazed at the people who are planting their feet to fight for something that what they were taught in third grade as if the world stopped there.
You’re right though. We should definitely teach different conventions. But then what would facebook do for engagement?
enforce writing math without ambiguity
It already is written without ambiguity.
were taught in third grade
This is actually taught in Year 7 - the people who only remember the 3rd Grade version of the rules are the ones getting it wrong.
There isn’t ambiguity to begin with - just people who have forgotten the rules of Maths.
What’s especially wild to me is that even the position of “it’s ambiguous” gets almost as much pushback as trying to argue that one of them is universally correct.
That’s because following the rules of Maths is universally correct.
arguing vehemently that implicit multiplication having precedence was correct and to do otherwise was wrong, full stop
He was using the wrong words, but he was correct - the actual rules are The Distributive Law and Terms (“implicit multiplication” is a rule made up by those who have forgotten these 2 rules).
Without any additional parentheses, the division sign is assumed to separate numerators and denominators within a complete expression, in which case you would reduce each separately. It’s very, very marginally ambiguous at best.
Assumed by whom? Clearly not everyone.
It’s what is actually taught in high school, so there are those who remember and those who don’t.
You are correct with your definition - Terms are separated by operators and joined by grouping symbols - and it’s consequently not ambiguous at all (using so-called “weak juxtaposition” breaks that rule).
The real lesson here is that clear, unambiguous communication is key.
And just what do you mean by that?
/s
It’s hilarious seeing all the genius commenters who didn’t read the linked article and are repeating all the exact answers and arguments that the article rebuts :)
I’m still not used to having combined image and text posts so I usually don’t notice the text portion if it isn’t a big ol’ wall and I hope I’m not the only one.
you are so sure that you are right and already “know it all”, why bother and even read this? There is no comment section to argue.
he made a mistake posting this to a comment section, now he must pay the price
❤️ True, but I think one of the biggest problems is that it’s pretty long and because you can’t really sense how good/bad/convining the text is it’s always a gamble for everybody if it’s worth reading something for 30min just to find out that the content is garbage.
I hope I did a decent job in explaining the issue(s) but I’m definitely not mad if someone decides that they are not going to read the post and still comment about it.
No, it doesn’t. It never talks about Terms, nor The Distributive Law (which isn’t the same thing as the Distributive Property). These are the 2 rules of Maths which make this 100% not ambiguous.
Just write it better.
6/(2(1+2))
Or
(6/2)(1+2)
That’s how it works in the real world when you’re using real numbers to calculate actual things anyways.
Meanwhile programmers will be like, fools, clearly
2(n)is a function 😏The only correct answer is
8008135.Oh i get it, if you flip that upside down it says “seiboob”
Which is French for “the boob”.
1337 5|*34X 15 [)34[) |V0\/\/ 83(4(_)53 0|= 70(_).
It sure is. 13 year old me would have no trouble deciphering this, but I only got up to [)34[).
Edit: I still got it. L337 H4xor PhoR L1F3
Leet speak is dead now because of you.
